Video of Torchbearer in action:

Project Summary:

The Torchbearer AI assists players in placing down torches to increase the light level of their surroundings. Our AI knows an optimal solution is n-coordinate large; thus it only tries the n-large combinations. We also create an sort algorithms to sort those combinations so that our AI tries the combinations those are close the center (the center can light up more area in a nXn size area ) first then tries the outside combinations.

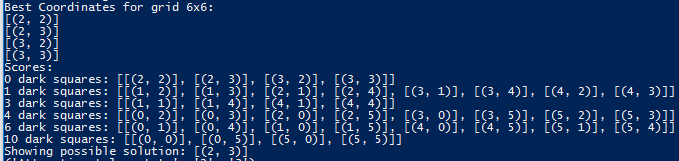
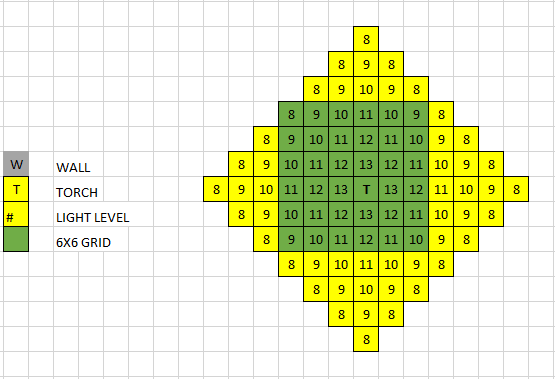
• A simple example of running our AI on a 6x6 square will place the torch in the center, therefore, it only costs one torch instead to place one torch on (1, 1), which requires at least two torches.
• 
• A simple example of running our AI on 9x9 area that requires at least two torches.
• 
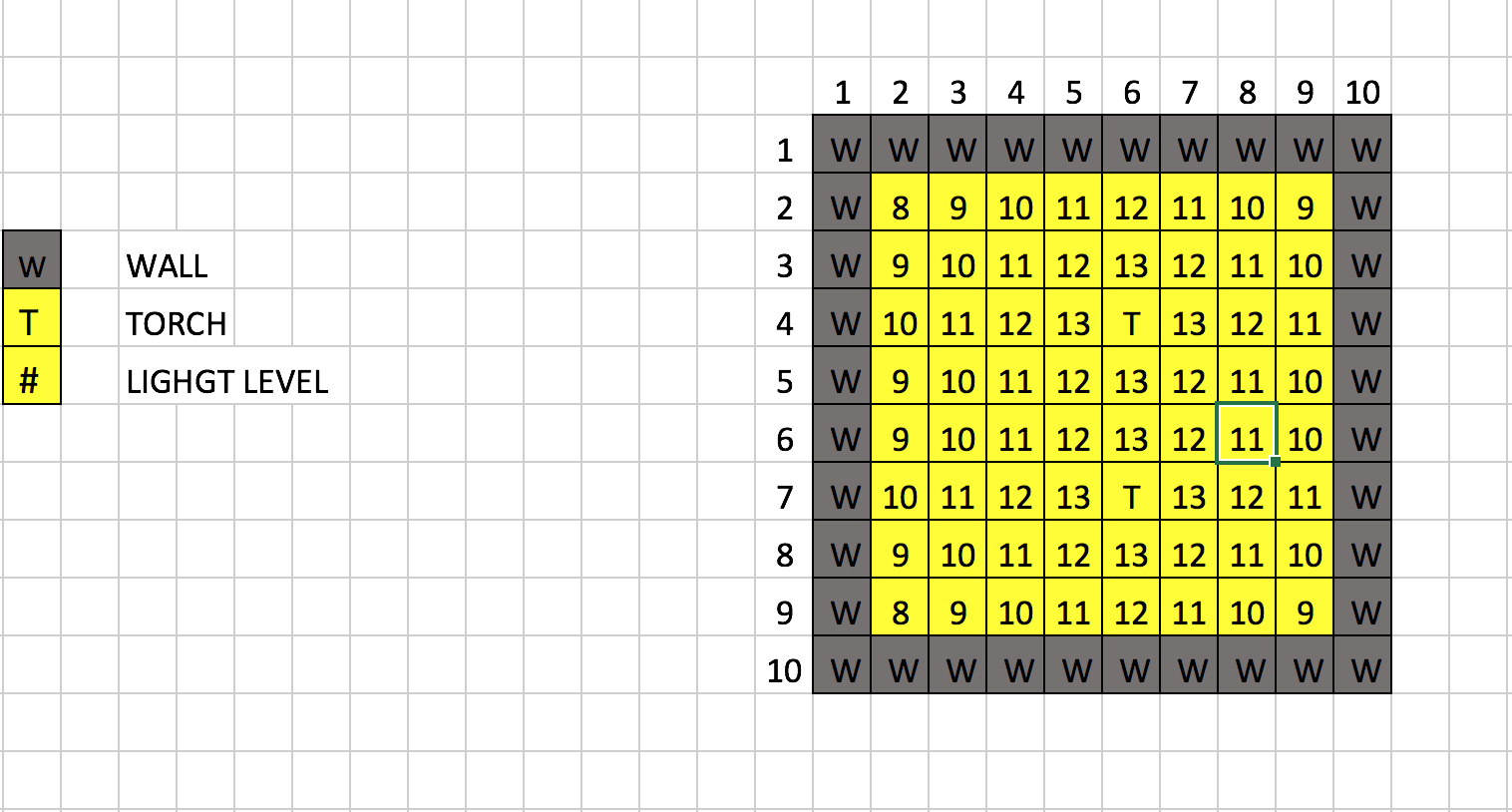
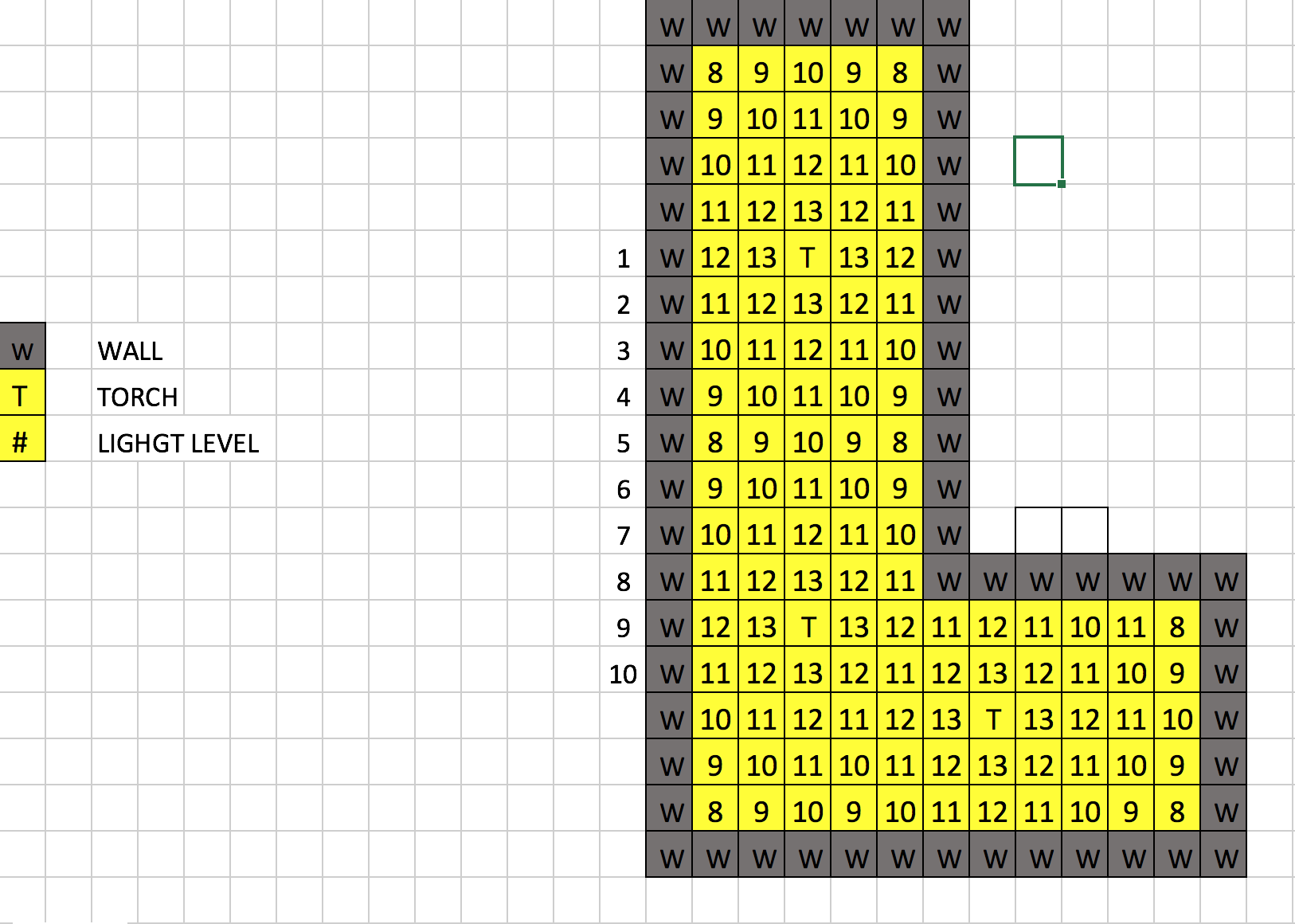
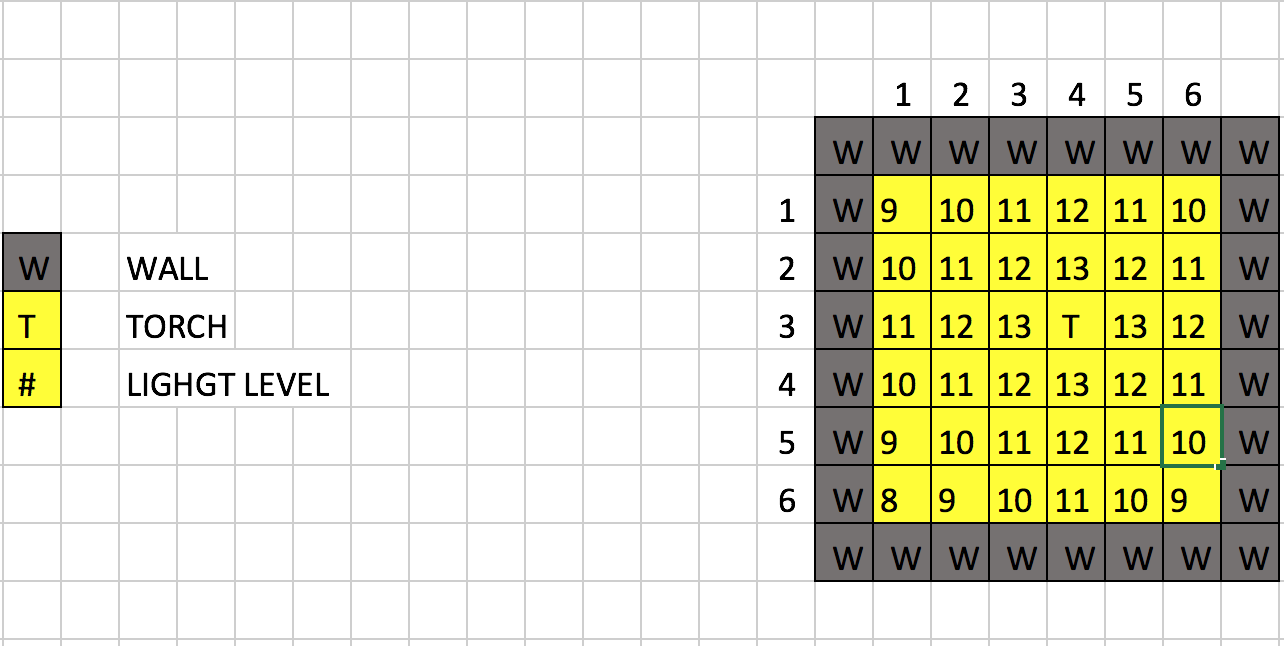
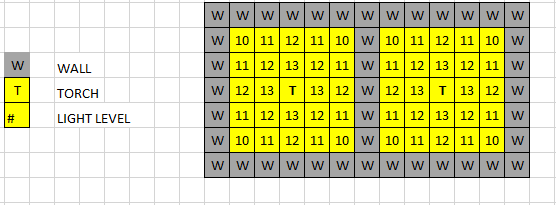
• Run the A.I. on grids with walls, the idea we mentioned previous has been achieved to find an optimal solution by our AI.
• 
• The non-uniform patterns are hard to determine how many torches can form the optimal solution; thus, our AI might take a longer time than the pattern before but our AI still can solve the problem we argued in the status report as following.
• 

Approach:

The Torchbearer A.I. determines the best locations to place torches in a grid by first determining the minimum amount of torches needed to light up the whole grid, then iterating over an n-sized combination of the valid coordinates of the grid, scoring each combination based on how many squares it left dark.

In order to find all optimal solutions, we use brute-force method in our AI to make sure we won’t miss any possible one. However, the brute-force is very expensive not only on the space but also the time cost; thus, we first use a math formula to calculate the number of torches of a optimal solutions.

• Min = Floor[(Number/2) - 2]
• Our baseline test – a 6x6 grid – works like this
  • In this case: 6/2 = 3; 3-2 = 1. Thus an optimal solution just needs one torch.
  • 
• The amount of available combinations (nCr) of coordinates is determined by the minimum torches needed (1) and the amount of spaces (36).
  • In this case: n = 36, r = 1 -> 36 unique 1-sized combinations of coordinates. This list of coordinates is named “startingList” for the moment.
  • We create a sort algorithm so that the 36 combinations is not just random but is ranked by their distance to the center of the square area
  • The sort result like [(2, 2), (2, 3), (3, 2), (1, 2), (2, 1), (0, 2), (1, 1), (1, 3), (2, 0), (2, 4), (3, 1), (3, 3), (4, 2), (0, 1), (0, 3), (1, 0), (1, 4), (2, 5), (3, 0), (3, 4), (4, 1), (4, 3), (5, 2), (0, 0), (0, 4), (1, 5), (3, 5), (4, 0), (4, 4), (5, 1), (5, 3), (0, 5), (4, 5), (5, 0), (5, 4), (5, 5)]
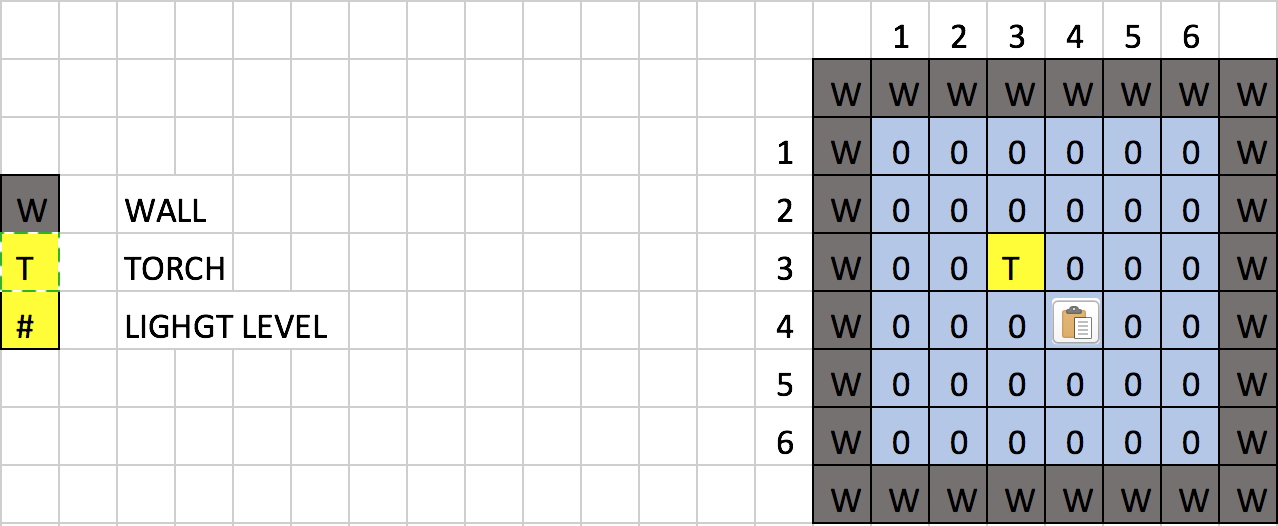
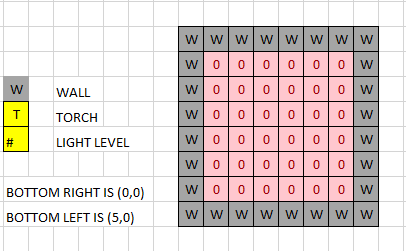
• The agent creates 6 lists, 6-size each, full of 0s to simulate the current light levels of the current test (named “currentList”).
• 
• The list of 36 combinations are then passed to the agent, who places a torch at each coordinate in the combination per test and checks the “score” of that placement:
• First, the agent teleports to coordinate (x, z). This torch’s coordinate in the “currentList” is determined first by its z-level, then by its x-level (so blocks at z-level 1 are in currentList[1]; a block at (3, 3) is at currentList[2][2]).
  • NOTE: Minecraft reads positive X going left, and positive Z going up. (Alternatively, positive X is going up, and positive Z is going right.)
• Then, the agent places a torch at its current position (3, 3), in the Minecraft world.
• After placing the torch, the agent updates what the new light levels of its surroundings should be.
  • The coordinate with the torch updates its number in “currentList” to 14 (“initialNum”).
  • 
  • For each coordinate in currentList that is not that coordinate, they update based on their taxicab distance away from the torch. This distance (“tryNum”) is equal to their difference in x coordinates + their difference in z coordinates.
  • 
  • An example of taxicab distance. The red, blue, and yellow lines all travel the same distance (12), while the green line is the unique solution that goes directly from point A to point B (approximately 8.49). (Image By User:Psychonaut - Created by User:Psychonaut with XFig, Public Domain, https://commons.wikimedia.org/w/index.php?curid=731390 )
  • The new light level of that specific coordinate is equal to “initialNum - tryNum” unless said light level would be lower than it currently is.
  • 
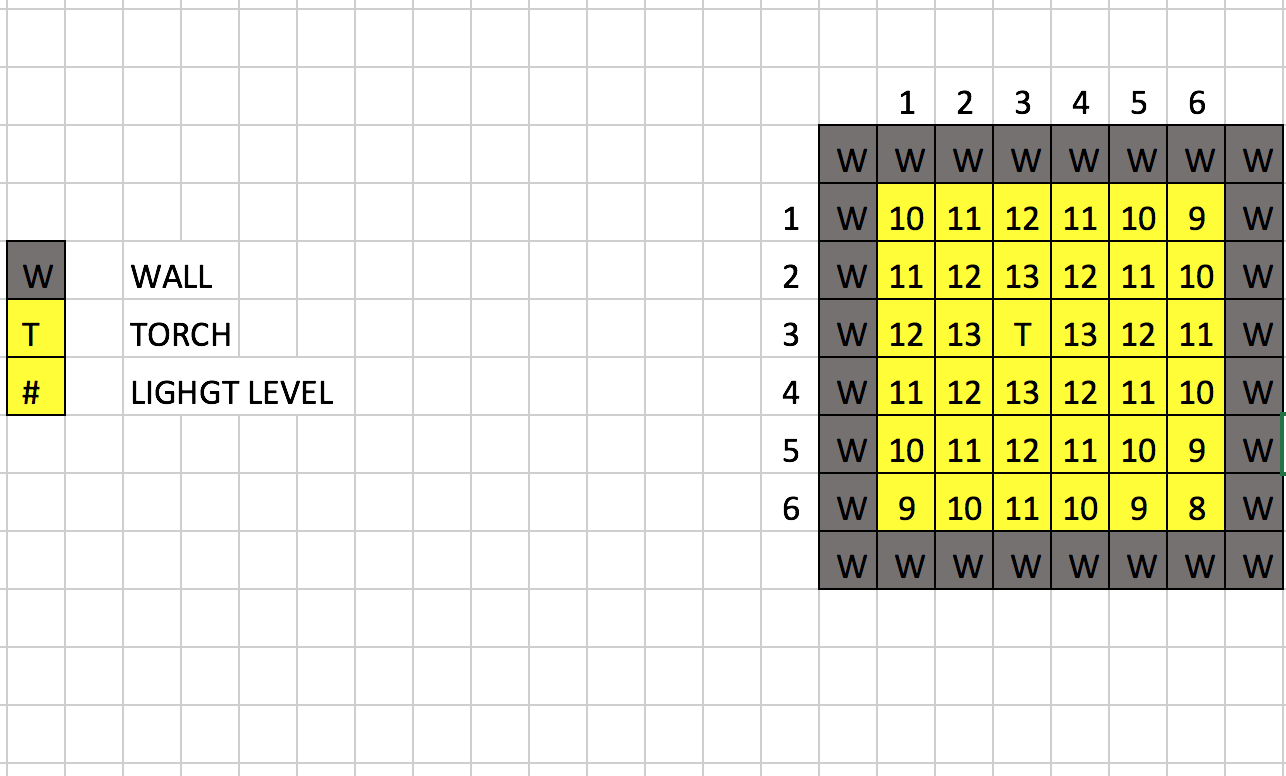
  • We get one solution! Cheers!
• Then, the AI will try the second combination which is (3, 4), in the Minecraft world.
  • It is the “currentList[2][3]” in our AI.
  • 
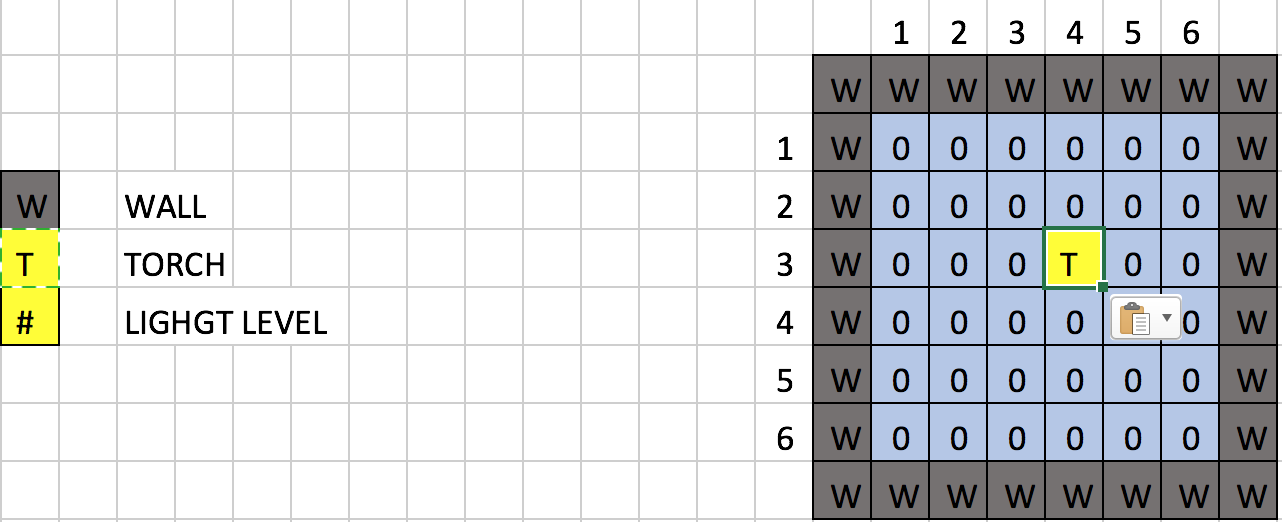
  • And after the update, the whole area will be lighted up like this.
  • 
  • Another solution! Cheers!
• After placing all of its torches within the combination it is testing, the agent then “scores” the combination based on how many squares remain in the grid that have a light level of 7 or below. This score is named “dark”.
• The combination is then placed into a dictionary “scoredList”, which has a variety of numeric keys and a list value. The combination is appended to the list with key “dark”; if that key does not exist, a new key is created with its value containing the combination.
  • An example of the “scoredList” would be scoredList[1] == [[(1, 2)], [(1, 3)], [(2, 1)], [(2, 4)], [(3, 1)], [(3, 4)], [(4, 2)], [(4, 3)]].
  • 
• The agent then wipes the board of all torches and begins the next test.
• After testing and scoring each coordinate in “startingList”, the program runs over each score in “scoredList” that has a list of coordinates (or a len > 0). If that score is the lowest so far, it updates a variable “lowest” to keep track of the list.
• Finally, the program runs over the list of the lowest scoring combinations, printing each one to show the optimal combinations to place torches to light up the grid (in this case: (2, 2), (2, 3), (3, 2), (3, 3)), as well as the entirety of “scoredList” for viewing purposes. The in-game agent places a combination as an example optimal solution.
• The approach we used in our AI have advantages like efficient on squared area and fast to find the solution but it is really hard to come up with a good algorithm to cope with the non-uniform pattern area, which means our AI still take some time to find the solutions for non-uniform pattern area.
• 
• 

Evaluation:

With the optimization to small-sized grids and weighting towards the center squares, the speed aspect of testing has dramatically improved. Now the A.I. no longer iterates over the entire combinatorial grid looking for a solution; instead, it looks for the first n^2 solutions using the center as the base, as opposed to the nCr amount of solutions that would arise (not a problem at n = 7, where r would then equal 1 and thus the set of possible solutions equals 49; definitely a problem at n = 10, where r would then equal 3 and the set of possible solutions equals 161700.)

However, this changes it from a complete A.I. to a merely fast one, and one that cannot effectively find the solutions at that. Better results could be found by iterating randomly over the set of solutions; definitive results could be found by iterating over all solutions. In short, we sacrificed completeness for speed, which unfortunately fails the criteria we set for the A.I.

One of the reasons we had a problem with attempting submodular optimization of the problem is that submodular optimization is NP-Hard. Each attempt at making two or more grids that are smaller than the nXn grid (but still covering the same area) requires just as much thought and calculation as does simply iterating over the whole nCr combinations.

References:

https://las.inf.ethz.ch/files/krause12survey.pdf (Paper on Submodular Optimization.)